Dynamic Fee Mechanism for Moonbeam
Hi, I’m Stephen (aka notlesh) from the Moonbeam core dev team. I focus a lot on the security of Moonbeam, which includes the various fee mechanisms we support.
Summary
This is a proposal to overhaul Moonbeam’s fee mechanism to adopt an algorithmic, congestion-based fee multiplier in the same spirit as EIP-1559. Instead of adopting the exact EIP-1559 algorithm, we use pallet-transaction-payment’s algorithm and translate it to an equivalent EIP-1559 base-fee for Ethereum transactions while carefully tuning the algorithm’s parameters to ensure that it remains feasible for all meaningful transactions.
Abstract
Moonbeam strives to bring full Ethereum compatibility to the Polkadot ecosystem. This means developing with a preference for strict compatibility but thoughtfully deviating when it makes sense. Our fee structure, especially as it relates to EIP-1559, is such a case where deviation is preferred.
Our fee mechanism is inherently a duality. We have the obvious goal of supporting Ethereum transactions and must live with its “upstream” design choices, but we are also a Substrate-based chain and inherit functionality from it which forces us to support a different transaction type. We call these two transaction types Substrate-based txns and Ethereum-based txns.
I have been working on a dynamic fee mechanism which supports both of these in a unified way for some time now and will describe its design and trade-offs here.
Where are we now?
Currently, Moonbeam supports Ethereum-based txns, including EIP-1559, EIP-2930, and legacy types. However, as I will explain later, we do not use the EIP-1559 dynamic base_fee. Instead, we ignore the specified gas price and use a fixed price of 1 gwei (Moonbase, Moonriver) and 100 gwei (Moonbeam). In addition, we consume any applicable priority fee (tip) but it is not paid to block authors.
We also support a rather “vanilla” pallet-base-fee implementation for Substrate-based txns, which includes a dynamic fee (although it doesn’t in any way impact Ethereum-based txns – something this proposal attempts to fix).
Why Not Just Use EIP-1559?
First, a quick refresher. EIP-1559 has a lot to it, but we’ll only focus on a few parts and leave most of it out of scope. Specifically, we care about:
-
base_fee: A strictly enforced fee charged for every transaction included in a block. An optional tip is supported, but otherwise this is exactly the fee that every txn in a block must pay. This is the “dynamic fee” in an EIP-1559 implementation. -
gas_limit: The max gas that can be used in a block. In the EIP, block authors may adjust this up or down by a small amount (at their discretion) in each block. -
gas_target: Defined as 50% ofgas_limit. This is the “congestion” target thatbase_feeresponds to. When a block uses more gas thangas_targetthebase_feeincreases and vice-versa.
Early on, supporting EIP-1559 was a goal. However, we knew immediately that we couldn’t implement 100% of the EIP. Specifically, we can’t fully implement the adjustable block gas_limit because Polkadot’s validator protocol would reject blocks if they are too big. This mechanism is directly related to the block gas_target in the EIP, so this also becomes questionable.
So what about the specific block base_fee adjustment? Well, this is closely related to the block gas_target, but perhaps we could use both a fixed gas_target and gas_limit and otherwise use the base_fee adjustment as prescribed.
In fact, this is actually what we started to do. The pallet-base-fee in frontier is exactly this. During our initial EIP-1559 support work, my colleague Telmo wrote a base-fee implementation which used fixed values for gas_target and gas_limit. But we were never comfortable enough with it to enable it, so it has remained disabled.
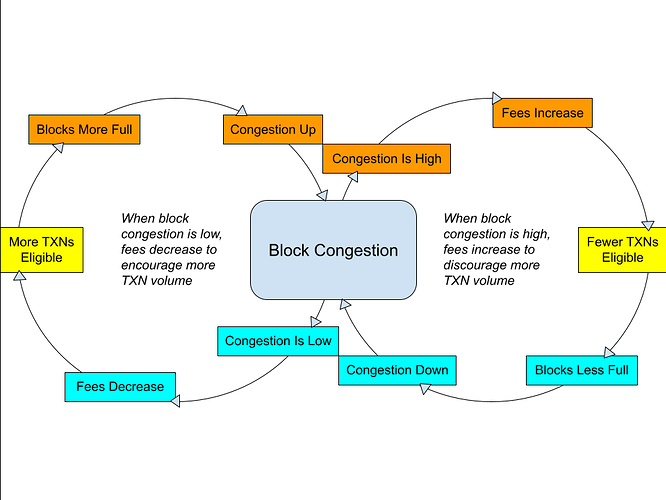
EIP-1559’s Feedback Loop
I like to think of the EIP’s design as a negative feedback loop whereby high txn congestion results in a dampening effect through increased pricing and vice versa:
This brings me to the rationale I have for not using EIP-1559:
- This feedback loop relies on a constant supply of transactions (or think of it as demand for block space). It is my opinion that EIP-1559 is inappropriate for any chain which cannot meet this requirement as the algorithm will not operate in equilibrium. Moonbeam’s networks have experienced periods of brief, intense congestion and periods of prolonged low congestion, which would not produce good results with this algorithm.
- The feedback loop is nuanced by adjustable
gas_targetandgas_limit, which we cannot implement in the same way. So we do not benefit from these mechanisms. - There are no guardrails built into this, so it becomes critical to tune things correctly otherwise
base_feewould drift up or down over time towards either 0 or infinity.
Substrate’s pallet-transaction-payment
An alternative that was discussed early on was to use the same dynamic fee mechanism that our Substrate-based transactions have been using this whole time. It turns out that it works similarly, at least at a high level. Congestion up -> price up, congestion down -> price down. It also has some compelling benefits:
- It was built for Substrate-based chains, and makes the general assumption that block space is fixed.
- It includes a lower and upper bound on its fee multiplier, so we don’t have to worry about txns becoming either free or impossibly expensive.
- The algorithm for adjusting fee from block to block is highly tunable, so we can tweak it based on real-world behavior.
This is the solution I am proposing: essentially we use pallet-transaction-payment’s algorithm and adjust its congestion-based multiplier to represent an equivalent EIP-1559 base-fee. From here we do the “normal” base-fee things with the caveat that the base-fee algorithm does not follow strict Ethereum consensus rules.
Brief Comparison of Transaction and Fee Structures
However, translating this fee mechanism for use with Ethereum-based transactions raises some concerns. Fundamentally, Substrate-based txns and Ethereum-based txns have vastly different fee mechanisms. pallet-transaction-payment’s fee multiplier can’t simply be converted to a base-fee without making some trade-offs. The fee structure is a bit out of scope, so I’ll describe the differences only briefly.
Ethereum’s fee mechanism includes concepts of base fee (21000 gas) and a length fee (input data is charged per-byte) and computation (the various costs per opcode). However, they are all lumped into the same category (“gas”) and then scaled by the base-fee multiplier to arrive at a final fee.
Substrate includes these same concepts, but each scales differently. Note that I am referring to Moonbeam’s current configuration; this will be different for other blockchains which use this pallet. Roughly, these are how things are scaled:
- base-fee is a constant
- length-fee is exponential (cheap for most txns, expensive for extremely large ones)
- computation is scaled by the multiplier
As you can imagine, converting this multiplier to a base fee is problematic because it impacts the two transaction types in different ways. In general, it will have a bigger impact on Ethereum fees than it will on Substrate ones.
Finding a Suitable Range
In order to make this work, we needed to understand what range, if any, we could use such that the multiplier would work reasonably well for both types of transactions. This was no easy feat, as the different parts of the fee created a sort of multi-dimensional space to consider. It was easy to tune for a specific txn “workload” (think: balance transfer) but this wouldn’t work well for different scenarios (such as an Ethereum create txn or a very large Substrate runtime-upgrade extrinsic).
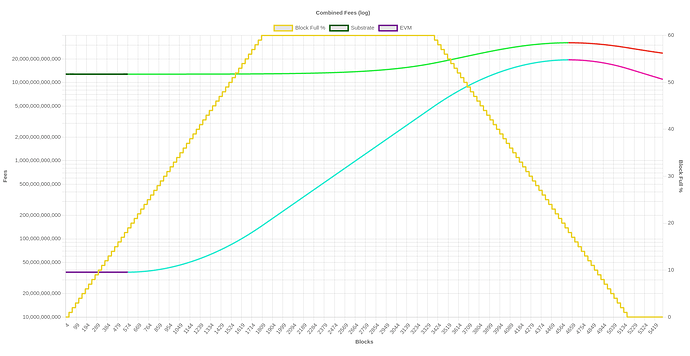
My colleague Nish did some excellent analysis of this problem by simulating the algorithm’s change over different ranges with different tuning parameters and then applying it to some specific transactions to compare its effects. This resulted in an ability to graph the multiplier across its range against theoretical transactions, allowing us to tune it so that the extremes were tenable.
In the example below, you can see a graph of comparable transactions (green/red: Substrate, blue/pink: Ethereum) graphed over a series of blocks where congestion is simulated by spamming junk txns (yellow: block congestion). In other words, we graph the cost of an Ethereum-based txn and a Substrate-based txn (which we think should be similar in fees) vs. the effect of the dynamic fee multiplier. As the congestion affects the multiplier, you see that it increases the cost of fees and causes both transaction types to converge in cost. This work helped us identify a usable range for setting upper/lower bounds in pallet-transaction-payment. You can also see the dynamic fees PR for some more discussion on this analysis.
Next steps
A snapshot voting session has been opened for 7 days here :
https://snapshot.org/#/moonbeam-foundation.eth/proposal/0x2ea736f08bdfc8a66935910b43afdf02486276de0e610f650711f9c51d2a9cb3
If the snapshot vote passes, this idea will be implemented and proposed to be included in one of the following Runtime Upgrade.
If you have any questions or comments, feel free to reply in the comment section below.